Numerical Study of the Influence of Droplet Injection Direction on Dust Particle Absorption

Full Text

ВВЕДЕНИЕ

В существующих исследованиях процессов жидкостной очистки запыленных сред наблюдается пренебрежение свойствами сжимаемости несущей среды или учетом эффектов взаимодействия несущей среды и дисперсной фазы. Также при теоретическом изучении динамики коагулирующих дисперсных включений для упрощения модели процессы коагуляции могут рассматриваться отдельно от газодинамических. Новизна работы заключается в учете взаимообратных эффектов взаимодействия дисперсных включений и несущей среды при моделировании вдува капельных потоков в запыленную среду под различными углами к стенке канала. Актуальность исследования связана с тем, что выявление закономерностей параметра вдува капельных фракций на интенсивность коагуляции позволит оптимизировать технологии жидкостной очистки газодисперсных сред.

Целью работы является исследование влияния угла вдува газокапельных фракций – φ в диапазоне π/6 ≤ φ ≤ 5π/6 на интенсивность коагуляции газокапельных фракций и пылевой фракции.

В рамках реализации цели предполагается проведение вычислительных экспериментов, в которых вдув капельных фракций в поток запыленной среды проводится под разными углами.

ОБЗОР ЛИТЕРАТУРЫ

Различные промышленные технологии часто связаны с течениями неоднородных сред [1–3]. Неоднородные среды могут быть смесями различных газов или многофазными течениями, в которых компоненты смеси отличаются агрегатным состоянием. Теоретической основой для динамики неоднородных сред, моделирования многофазных течений служат фундаментальные исследования в этой области¹. Разработаны континуальные методики описания таких систем, а также расчетные методы моделирования многофазных газожидкостных сред². Проблемы математического моделирования ударно-волновых процессов в многофазных средах нашли отражение в ряде научных школ. Так, Новосибирские ученые рассмотрели теоретические аспекты и получили физические параметры ударных волн в газовзвесях³. Одномерные математические модели ударно-волновой динамики запыленных, газокапельных и порошковых сред, разработанные А. Г. Кутушевым, а также ударно-волновые и детонационные течения металлических частиц в газе, исследованные А. В., Федоровым, В. М. Фоминым, Т. А. Хмель представляют комплексный подход к изучению многофазных сред⁴. А. Ю. Вараксин провел обзор и анализ теоретических и экспериментальных исследований потоков неоднородных газодисперсных сред, в частности, направленных на изучение взаимодействия газа и дисперсных частиц, где автор отмечает преимущество континуальных моделей при моделировании дисперсных потоков с большим объемным содержанием дисперсных частиц [2]. М. А. Пахомовым, В. И. Тереховым на основе численных методов проанализирован процесс распространения дисперсной примеси в трубе, а также рассмотрен теплообмен между фазами смеси [3]. С помощью физического моделирования исследовано влияние вдува на параметры течения газа с твердыми частицами и на скоростные параметры частиц различных размеров, предложено практическое применение выявленных физических закономерностей для защиты поверхностей от дисперсных потоков твердых частиц [4]. В рамках численного моделирования исследовано течение смеси газа и твердых частиц в канале с проницаемыми стенками и описаны процессы, происходящие в камере сгорания твердотопливного ракетного двигателя [5].

Проблемы математического моделирования эффективности скрубберов были рассмотрены в исследованиях, в которых предложен ряд методов повышения эффективности устройств [6]. В работе зарубежных ученых экспериментально изучено влияние коагуляции и седиментации на процесс очитки аэрозолей, образующихся при выбросе продуктов работы атомных электростанций в атмосферу [7]. В свою очередь А. А. Шрайбер, И. В. Фединчик и М. В. Протасов разработали модель динамики полидисперсной газовзвеси в скруббере Вентури с использованием физических упрощений в предположении одномерной геометрии и стационарного характера течения [8]. Учеными из Уральского горного университета были проведены исследования закономерностей динамики вращающихся капель жидкости, по результатам которых разработана математическая модель их циркуляционного движения в газовой среде [9]. На основе уравнения Буссинеска построена математическая модель движения пылевых частиц в аппарате жидкостной очистки, также разработаны критерии подобия физических экспериментов и процессов в реальных условиях шахт [10]. Результаты исследования влияния гидродинамических взаимодействий на скорость коагуляции частиц представлены в трудах авторов из США [11]. В расчетах предполагалась сферическая форма дисперсных включений. Процесс коагуляционного столкновения двух капель криогенной жидкости при низких температурах, а также двух капель воды при комнатных температурах при различных числах Рейнольдса и параметров удара был описан учеными из Китая, однако их математическая модель пренебрегала сжимаемостью среды [12]. В настоящее время разработана математическая модель потока многофазной среды при наличии процессов нуклеации, коагуляции и фазовых переходов, где для описания первого используется модель гомогенной нуклеации [13].

Математически смоделирован процесс жидкостной очистки запыленной среды в трубе Вентури, где за счет воздействия ультразвука происходит интенсификация процесса коагуляции, однако не учитывается воздействие дисперсной фазы на динамику несущей среды [14]. М. В. Тимофеева представила математическую модель процесса коагуляции капель нескольких фракций, отличающихся размером в технологии аэрохолодильного охлаждения без расчетов и моделирования газодинамических процессов несущей среды [15].

Китайскими учеными исследованы процессы столкновения и коагуляции дисперсных частиц, смоделированы процессы коагуляция капель воды, взвешенных в атмосфере [16]. Исследователи из Южной Африки провели расчеты рабочих режимов скруббера методами вычислительной гидродинамики; несущая среда описывалась ими полной гидродинамической системой уравнений, а для описания параметров дисперсной фазы решались обыкновенные дифференциальные уравнения относительно временной переменной с учетом параметров воздействия на дисперсные частицы со стороны несущей среды. Так, пренебрегались эффекты взаимообратного воздействия компонент смеси [17].

Австрийскими учеными разработана математическая модель расчетных соотношений процессов массопереноса в скрубберах, используемых в химической промышленности, без учета гидродинамических процессов [18].

Исследователи из Индии привели обзор публикаций, посвященных проблемам работы скрубберов, и проанализировали влияние различных гидродинамических параметров на эффективность работы этих устройств, отмечая важность вычислительной гидродинамики для оптимизации работы этих аппаратов [19].

В публикациях, посвященных динамике газовзвесей, исследуются различные вопросы, связанные с практическими приложениями. В частности, интерес к исследованию коагулирующих частиц связан с промышленной энергетикой и аэрокосмической техникой⁵. Актуальность исследования динамики коагуляции дисперсных сред обусловлена повышением производительности оборудования для очистки запыленных сред от дисперсных включений.

Анализ литературы демонстрирует, что при моделировании течений многофазных сред исследователи часто пренебрегают либо сжимаемостью несущей среды, либо межфазным взаимодействием. В ряде случаев течение описывается как стационарное течение с одномерной геометрией, при этом описание двухмерных эффектов важно при исследовании вдува капельных фракций поперек потока запыленной среды. При моделировании процессов коагуляции в многофазных средах не учитывается межфазное взаимодействие или в целом рассматриваются процессы коагуляции без расчета газодинамических уравнений.

МАТЕРИАЛЫ И МЕТОДЫ

На данный момент при описании неоднородных сред применяется несколько подходов: равновесный, предполагающий описание течения неоднородной среды как однородной с введением поправок на ее неоднородность⁶; диффузионный, наиболее подходящий для описания течений гомогенных смесей, имеющих одинаковое агрегатное состояние, например, смесей газов. В расчетах применялась компьютерная программа, реализующая численное решение для континуальной математической модели динамики многофазных сред. Дисперсная фаза предполагалась полидисперсной и многофракционной с учетом различных размеров дисперсных включений плотности и теплоемкости фракций дисперсной фазы [20]. Уравнения математической модели учитывали тепловое и скоростное взаимодействие фракций дисперсной фазы и несущей среды. Газовая фаза смеси описывалась системой уравнений Навье – Стокса с учетом теплообмена и обмена импульсом с фракциями дисперсной фазы [21–23]:

$\frac{\partial \left(\left(1-{\displaystyle \sum _{i=2}^n{\alpha }_i}\right){\rho }_1\right)}{\partial t}+\frac{\partial \left(\left(1-{\displaystyle \sum _{i=2}^n{\alpha }_i}\right){\rho }_1{u}_1\right)}{\partial x}+\frac{\partial \left(\left(1-{\displaystyle \sum _{i=2}^n{\alpha }_i}\right){\rho }_1{v}_1\right)}{\partial y}=\mathrm{0,}$

$\frac{\partial \left({\rho }_1{u}_1\right)}{\partial t}+\frac{\partial }{\partial x}\left({\rho }_1{u}_1^2+p-{\tau }_{xx}\right)+\frac{\partial }{\partial y}\left({\rho }_1{u}_1{v}_1-{\tau }_{xy}\right)=-{\displaystyle \sum _{i=\mathrm{2,}n}{F}_{xi}}+{\displaystyle \sum _{i=\mathrm{2,}n}{\alpha }_i\frac{\partial p}{\partial x}},$

$\frac{\partial \left({\rho }_1{v}_1\right)}{\partial t}+\frac{\partial }{\partial x}\left({\rho }_1{u}_1{v}_1-{\tau }_{yx}\right)+\frac{\partial }{\partial y}\left({\rho }_1{v}_1^2+p-{\tau }_{yy}\right)=-{\displaystyle \sum _{i=\mathrm{2,}n}{F}_{yi}}+{\displaystyle \sum _{i=\mathrm{2,}n}{\alpha }_i\frac{\partial p}{\partial y}},$

${\tau }_{xx}=\mu \left(2\frac{\partial u_1}{\partial x}-\frac{2}{3}D\right)\text{, }{\tau }_{yy}=\mu \left(2\frac{\partial v_1}{\partial y}-\frac{2}{3}D\right),$

${\tau }_{xy}=\mu \left(\frac{\partial u_1}{\partial y}+\frac{\partial v_1}{\partial x}\right), D=\frac{\partial u_1}{\partial x}+\frac{\partial v_1}{\partial y},$  

где n – количество фракций, α_i – объемное содержание i-ой фракции; ρ₁ – средняя плотность газа, кг/м³; t – время, с; u₁, v₁ – декартовы составляющие скорости несущей среды, м/с; x – продольная координата, м; y – поперечная координата, м; p – давление, Па; τ_xx, τ_xy, τ_yx, τ_yy – составляющие тензора вязких напряжений, Па; F_xi  и F_yi – х и у составляющие межфазного обмена импульсом i-ой фракции, кг/(м²·с²); e₁ – полная энергия несущей среды, Дж; λ – теплопроводность газа, Вт/(м·К); T₁ – температура несущей среды, К; Q_i – тепловой поток между i-ой фракцией и несущей средой, Дж/c; u_i –составляющая скорости i-ой фракции в х направлении м/с.; v_i – составляющая скорости i-ой фракции в у направлении м/с; μ – динамическая вязкость газа, Па·с; D – вспомогательная функция, c^–1.

В работе предполагалось, что плотность несущей среды ρ₁ определяется исходя из ее объемного содержания α₁ и физической плотности несущей среды ρ_g0: ${\rho }_1\left(x,y\right)={\alpha }_1\left(x,y\right){\rho }_{g0}$, ρ_g0 – начальная физическая плотность газа, кг/м³.

Для моделирования динамики i-ой фракции дисперсной фазы применялась полная система уравнений динамики сплошной среды [24; 25]:

$\frac{\partial {\rho }_i}{\partial t}+\frac{\partial \left({\rho }_i{u}_i\right)}{\partial x}+\frac{\partial \left({\rho }_i{v}_i\right)}{\partial y}=\mathrm{0,}$

 $\frac{\partial \left({\rho }_i{u}_i\right)}{\partial t}+\frac{\partial }{\partial x}\left({\rho }_i{u}_i^2\right)+\frac{\partial }{\partial y}\left({\rho }_i{u}_i{v}_i\right)=F_{xi}-{\alpha }_i\frac{\partial p_{}}{\partial x},$ 

 $\frac{\partial \left({\rho }_i{v}_i\right)}{\partial t}+\frac{\partial }{\partial x}\left({\rho }_i{u}_i{v}_i\right)+\frac{\partial }{\partial y}\left({\rho }_i{v}_i^2\right)=F_{yi}-{\alpha }_i\frac{\partial p_{}}{\partial y},$ 

$\frac{\partial \left(e_i\right)}{\partial t}+\frac{\partial }{\partial x}\left(e_i{u}_i\right)+\frac{\partial }{\partial y}\left(e_i{v}_i\right)=-Q_i,$

 ${\rho }_i={\alpha }_i{\rho }_{i0},e_i={\rho }_i{C}_{vi}{T}_i,$ 

 $\begin{array}{l}{F}_{yi}=\frac{3}{4}\frac{{\alpha }_i}{d_i}{C}_d{\rho }_1\sqrt{{\left(u_1-u_i\right)}^2+{\left(v_1-v_i\right)}^2}\left(v_1-v_i\right)+{\alpha }_i{\rho }_1\left(\frac{\partial v_1}{\partial t}+u_1\frac{\partial v_1}{\partial x}+v_1\frac{\partial v_1}{\partial y}\right)+\\ +\mathrm{0,5}{\alpha }_i{\rho }_1\left(\frac{\partial v_1}{\partial t}+u_1\frac{\partial v_1}{\partial x}+v_1\frac{\partial v_1}{\partial y}-\frac{\partial v_i}{\partial t}-u_i\frac{\partial v_i}{\partial x}-v_i\frac{\partial v_i}{\partial y}\right),\end{array}$ 

$$\begin{gathered} C_{di}^{}=\frac{\text{24}}{R{e}_{i1}}+\frac{\text{4}}{R{e}_{i1}^{\text{0}\text{,5}}}+\text{0}\text{,4}\text{, }{\displaystyle {{\displaystyle M}}_{i1}}{\displaystyle =}{\displaystyle \frac{\left|{\overline{V}}_1-{\overline{V}}_i\right|}{c}}{\displaystyle ,} \\ {\displaystyle {{\displaystyle \mathrm{Re}}}_{i1}}{\displaystyle =}{\displaystyle \frac{{\rho }_1\left|{\overline{V}}_1-{\overline{V}}_i\right|d_i}{\mu }}{\displaystyle \text{, }}{\displaystyle \mathrm{Pr}}{\displaystyle =}{\displaystyle \frac{C_p\mu }{\lambda }}{\displaystyle ,} \end{gathered}$$

$N{u}_i=2\exp \left(-M_{i1}\right)+\mathrm{0,459}{M}_{i1}^{\mathrm{0,55}}P{r}^{\mathrm{0,33}},$

$Q_i=Q_i=\frac{6{\alpha }_i\lambda N{u}_i\left(T_1-T_i\right)}{d_i{}^2},i=\mathrm{2,}\mathrm{...,}n,$

где ρ_i – средняя плотность i-ой фракции дисперсной фазы, кг/м³; e_i – тепловая энергия i-ой фракции дисперсной фазы, Дж; ρ_i0 – физическая плотность i-ой фракции дисперсной фазы, кг/м³; C_vi – теплоемкость материала i-ой фракции дисперсной фазы, Дж/(кг·К); T_i – температура несущей среды дисперной фазы, К; d_i – диаметр частицы i-ой фракции дисперсной фазы, м; C_di – коэффициент сопротивления i-ой фракции дисперсной фазы; Re_i1 – относительное число Рейнольдса i-ой фракции; M_i1 – относительное число Маха i-ой фракции дисперсной фазы; V₁ – вектор скорости несущей среды, м/с; V_i – вектор скорости i-ой фракции дисперсной фазы, м/с; c – скорость звука в м/с; Pr – число Прандтля; C_p – теплоемкость, Дж/(кг·К); Nu_i – относительное число Нуссельта i-ой фракции дисперсной фазы.

Обмен импульсом i-ой фракции дисперсной и газовой фазы учитывал несколько различных сил: силу аэродинамического сопротивления F_AD, динамическую силу Архимеда F_DA, силу присоединенных масс F_MA в продольном и поперечном направлении соответственно х и у:

$F_{ADxi}=\frac{3}{4}\frac{{\alpha }_i}{d_i}{C}_d{\rho }_1\sqrt{{\left(u_1-u_i\right)}^2+{\left(v_1-v_i\right)}^2}\left(u_1-u_i\right),$

$F_{DAxi}={\alpha }_i{\rho }_1\left(\frac{\partial u_1}{\partial t}+u_1\frac{\partial u_1}{\partial x}+v_1\frac{\partial u_1}{\partial y}\right),$

$F_{AMxi}=\mathrm{0,5}{\alpha }_i{\rho }_1\left(\frac{\partial u_1}{\partial t}+u_1\frac{\partial u_1}{\partial x}+v_1\frac{\partial u_1}{\partial y}-\frac{\partial u_i}{\partial t}-u_i\frac{\partial u_i}{\partial x}-v_i\frac{\partial u_i}{\partial y}\right),$

$F_{ADyi}=\frac{3}{4}\frac{{\alpha }_i}{d_i}{C}_d{\rho }_1\sqrt{{\left(u_1-u_i\right)}^2+{\left(v_1-v_i\right)}^2}\left(v_1-v_i\right),$

$F_{DAyi}={\alpha }_i{\rho }_1\left(\frac{\partial v_1}{\partial t}+u_1\frac{\partial v_1}{\partial x}+v_1\frac{\partial v_1}{\partial y}\right),$

$F_{AMyi}=\mathrm{0,5}{\alpha }_i{\rho }_1\left(\frac{\partial v_1}{\partial t}+u_1\frac{\partial v_1}{\partial x}+v_1\frac{\partial v_1}{\partial y}-\frac{\partial v_i}{\partial t}-u_i\frac{\partial v_i}{\partial x}-v_i\frac{\partial v_i}{\partial y}\right),$

где F_ADxi – x составляющая силы аэродинамического сопротивления i-ой фракции,  кг/(м²·с²); F_DAxi – х составляющая динамической силы Архимеда i-ой фракции, кг/(м²·с²); F_AMxi – х составляющая силы присоединенных масс i-ой фракции, кг/(м²·с²); F_ADyi – y составляющая силы аэродинамического сопротивления i-ой фракции, кг/(м²·с²); F_DAyi – y составляющая динамической силы Архимеда i-ой фракции, кг/(м²·с²); F_AMyi – y составляющая силы присоединенных масс i-ой фракции, кг/(м²·с²).

Использовалась модель столкновительной коагуляции дисперсных включений, описанная В. Е. Алемасовым^[7] [20]:

$\frac{\partial m_i}{\partial t}={\displaystyle \sum _{j=2}^{i-1}{k}_{ij}{n}_j}{m}_j\text{, }$

$k_{ij}=\frac{\pi }{4}{\left(d_i+d_j\right)}^2\left[u_{i}cos\left(\theta \right)+v_{i}sin\left(\theta \right)-\sqrt{u_j^2+v_j^2}\right],\theta =arctg\left(\frac{v_j}{u_j}\right).$

$\frac{\partial n_i}{\text{d}t}=-n_i{\displaystyle \sum _{j=i+1}^n{k}_{ij}{n}_j}\text{,}$ 

$\begin{array}{l}\frac{\partial u_{\text{i}}}{\text{d}t}=\frac{1}{m_i}{\displaystyle \sum _{j=2}^{i-1}{k}_{ij}\left(u_j-u_i\right)m_j{n}_j}\text{,}\\ \frac{\partial v_{\text{i}}}{\text{d}t}=\frac{1}{m_i}{\displaystyle \sum _{j=2}^{i-1}{k}_{ij}\left(v_j-v_i\right)m_j{n}_j}\text{,}\end{array}$

$T_{i*}=\frac{1}{C_i{m}_{i*}}\left({\displaystyle \sum _{j=2}^{i-1}{k}_{ij}{n}_j{C}_j}{m}_j{T}_j+C_i{m}_i{T}_i\right)\text{.}$

где d – диаметр капли, м; m_i – масса частицы i-й фракции, кг; ρ_i0 – средняя плотность фракции дисперсной фазы, кг; k_ij – константа коагуляции, м²·с; n_j – концентрация, м⁻³; m_j – масса j-ой фракции, кг; d_j – диаметр капли j-ой фракции, м; u_j – х составляющая скорости j-ой фракции, м/с; v_j – y составляющая скорости j-ой фракции, м/с; n_i – концентрация частиц i-й фракции, м⁻³; T_i* – температура частицы i-й фракции после коагуляции, К; C_i*, C_j, C_i – теплоемкость i-й фракции, Дж/(кг·К); m_i* – масса i-ой фракции, кг; T_j – температура i-й фракции К.

Предполагается, что частицы i-й фракции поглощают все частицы меньших размеров, т. е. частицы фракций j = 2…i – 1.

Системы уравнений динамики полидисперсной газовзвеси (1) – (2) интегрировались конечно-разностным методом Мак-Кормака второго порядка точности⁸.

Рассмотрим применение численного алгоритма явного метода Мак-Кормака на примере скалярного нелинейного уравнения в частных производных (3):

Алгоритм явного конечно-разностного метода Мак-Кормака для скалярного нелинейного уравнения (3) имеет вид (4)–(5):

где Δх, Δy – шаги по пространственному направлению, Δt – шаг по времени, bn_j,k+1.

В явном методе Мак-Кормака в качестве условия устойчивости рассматривается условие устойчивости типа Куранта – Фридрихса – Леви⁹:

$\Delta t\le \frac{\Delta h^2}{4\nu \text{+}\left(\left|u\right|+\left|v\right|\right)\Delta h}\text{,}\Delta h=\text{min}\left(\Delta x,\Delta y\right)\text{, }\left|u\right|=\text{max}\left|u_i\right|,\left|v\right|=\text{max}\left|v_i\right|$

Численные осцилляции преодолевались с помощью схемы нелинейной коррекции сеточной функции [26; 27]: если $\left(\delta {\tilde{u}}_{j-1/2}\cdot \delta {\tilde{u}}_{j+1/2}\right)<0$ или $\left(\delta {\tilde{u}}_{j+1/2}\cdot \delta {\tilde{u}}_{j+3/2}\right)<0,$ то $f_j{\displaystyle =}{\displaystyle {\tilde{f}}_j}{\displaystyle +}{\displaystyle k}{\displaystyle \left(\delta u_{j+1/2}-\delta u_{j-1/2}\right)}$. Использованы обозначения: $\delta {\tilde{u}}_{j-1/2}={\tilde{u}}_j-{\tilde{u}}_{j-1}$, $\delta {\tilde{u}}_{j+1/2}={\tilde{u}}_{j+1}-{\tilde{u}}_j$, $\delta {\tilde{u}}_{j+3/2}={\tilde{u}}_{j+2}-{\tilde{u}}_{j+1},$  где ${\tilde{u}}_j$ – значение функции после перехода на (n+1)-ый временной слой по схеме Мак-Кормака, коэффициент коррекции – k = 0,125.

Сопоставление численной модели с результатами физического эксперимента дало приемлемое соответствие [25].

В данной работе численно моделируется динамика газовзвесей в вязком сжимаемом теплопроводном газе.

Рассматривались углы вдува как по направлению течение пылевой фракции, так и случаи, когда потоки газокапельных фракцию втекают против потока пылевой фракции.

В численных расчетах задавались следующие граничные условия:

$u_1\left(t\mathrm{,1,}j\right)=u_0\text{,}{u}_2\left(t\mathrm{,1,}j\right)=u_0\text{,}{u}_k\left(t\mathrm{,1,}j\right)=u_k\left(t\mathrm{,2,}j\right), v_k\left(t\mathrm{,1,}j\right)=\mathrm{0,}$

$u_k\left(t\text{, }{N}_x\text{, }j\right)=\mathrm{0,} v_k\left(t\text{, }{N}_x\text{, }j\right)=v_k\left(t\text{, }{N}_x-\mathrm{1,}j\right)\text{, }$

$u_k\left(t\text{, }i\text{, }{N}_y\right)=\mathrm{0,}{v}_k\left(t\text{, }i\text{, }{N}_y\right)=\mathrm{0,} u_k\left(t\text{, }i\text{, }1\right)=\text{0, }{v}_k\left(t\text{, }i\text{, }1\right)=\mathrm{0,}$

$u_k\left(t\text{, }i\text{, }1\right)=\mathrm{0,} v_2\left(t\text{, }i\text{, }1\right)=v_2\left(t\text{, }i\text{, }2\right)\text{,\hspace{1em}}{v}_k\left(t\text{, }i\text{, }1\right)=v_0\text{, }$ 

${\rho }_1\left(t\mathrm{,1,}j\right)={\rho }_1\left(t\mathrm{,2,}j\right)\text{,}{\rho }_2\left(t\mathrm{,1,}j\right)={\rho }_{20}{\alpha }_{20}\text{, }{\rho }_k\left(t\mathrm{,1,}j\right)={\rho }_k\left(t\mathrm{,2,}j\right)\text{, }$

${\rho }_k\left(t\text{, }{N}_x\text{, }j\right)={\rho }_k\left(t\text{, }{N}_x-\mathrm{1,}j\right)\text{, }{\rho }_1\left(t\text{,}i\mathrm{,1}\right)={\rho }_1\left(t\text{,}i\mathrm{,2}\right)\text{,\hspace{1em}}{\rho }_k\left(t\text{,}i\mathrm{,1}\right)={\rho }_k\left(t\text{,}i\mathrm{,2}\right)\text{,}$

${\rho }_1\left(t\text{,}i\text{,}{N}_y\right)={\rho }_1\left(t\text{,}i\text{, }{N}_y-1\right)\text{,}{\rho }_k\left(t\text{,}i\text{,}{N}_y\right)={\rho }_k\left(t\text{,}i\text{,}{N}_y-1\right)\text{, }$

$e_1\left(t\mathrm{,1,}j\right)=e_1\left(t\mathrm{,2,}j\right)\text{, }{e}_k\left(t\mathrm{,1,}j\right)=e_k\left(t\mathrm{,2,}j\right)\text{,}$

$e_1\left(t\text{,}{N}_x\text{, }j\right)=e_1\left(t\text{,}{N}_x-\mathrm{1,}j\right)\text{,}{e}_k\left(t\text{,}{N}_x\text{, }j\right)=e_k\left(t\text{,}{N}_x-\mathrm{1,}j\right)\text{,}$

$e_1\left(t\text{,}i\mathrm{,1}\right)=e_1\left(t\text{,}i\mathrm{,2}\right)\text{,}{e}_k\left(t\text{,}i\mathrm{,1}\right)=e_k\left(t\text{,}i\mathrm{,2}\right)\text{,}$

$e_1\left(t\text{,}i\text{, }{N}_y\right)=e_1\left(t\text{,}i\text{, }{N}_y-1\right)\text{,}{e}_k\left(t\text{,}i\text{,}{N}_y\right)=e_k\left(t\text{,}i\text{,}{N}_y-1\right)\text{,}$

$p\left(t\mathrm{,1,}j\right)=p\left(t\mathrm{,2,}j\right)\text{, }p\left(t\text{,}{N}_x\text{, }j\right)=p\left(t\text{,}{N}_x-\mathrm{1,}j\right)\text{, }p\left(t\text{,}i\mathrm{,1}\right)=p\left(t\text{,}i\mathrm{,2}\right)\text{,}$

$p\left(t\text{,}i\text{,}{N}_y\right)=p\left(t\text{,}i\text{,}{N}_y-1\right),$     

где u₀ – продольная скорость втекания запыленной среды в канал, м/c.

Граничные условия на поверхности вдува описывают впрыск капельного потока под углом φ к стенке канала:

$L_1\le i\Delta x\le L_2$

${\rho }_1\left(t\text{,}i\mathrm{,1}\right)={\rho }_1\left(t\text{,}i\mathrm{,2}\right)\text{,}{\rho }_2\left(t\text{,}i\mathrm{,1}\right)={\rho }_2\left(t\text{,}i\mathrm{,2}\right)\text{,}{\rho }_k\left(t\text{,}i\mathrm{,1}\right)={\rho }_{k0}\text{, }$

$u_1\left(t\text{,}i\mathrm{,1}\right)=v_{0}cos\phi \text{,}{u}_k\left(t\text{,}i\mathrm{,1}\right)=v_{0}cos\phi \text{,}{v}_1\left(t\text{,}i\mathrm{,1}\right)=v_{0}sin\phi \text{,}{v}_k\left(t\text{,}i\mathrm{,1}\right)=v_{0}sin\phi \text{, }$

$v_2\left(t\text{,}i\mathrm{,1}\right)=v_2\left(t\text{,}i\mathrm{,2}\right), p\left(t\text{,}i\mathrm{,1}\right)=p\left(t\text{,}i\mathrm{,2}\right),$

где v₀ – поперечная скорость втекания капельных фракций через поверхность вдува, м/c.

Количество узлов и их нумерация в х и у направлениях – N_x = 200, N_y = 100, i, j.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

С целью определения влияние угла вдува капельных фракций на интенсивность коагуляции было проведено несколько вычислительных экспериментов по моделированию коагуляции пылевых частиц и капельных фракций с различными параметрами вдува капельных фракций.

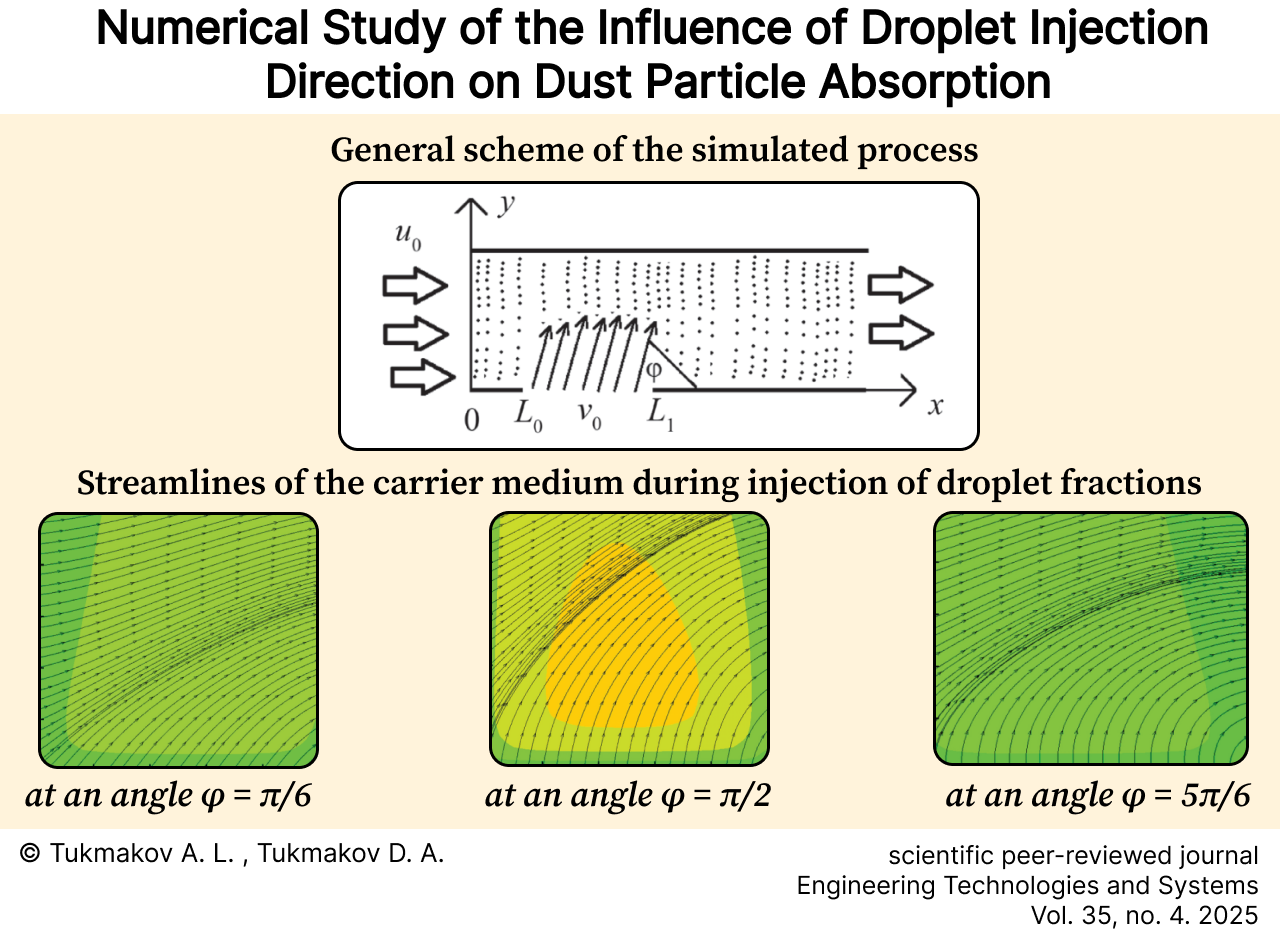
На рисунке 1 схематично изображен моделируемый процесс вдува капельных фракций в поток запыленной среды. Газовая фаза смеси и пылевая фракция дисперсной фазы движутся в продольном направлении со скоростью u₀ = 20 м/с. Четыре капельных фракции с разными размерами капель вдуваются через боковую поверхность. Капельные фракции вдуваются со скоростью v₀ = 4 м/с под углом φ к поверхности канала. Параметры физической области: длина канала L = 0,4 м, ширина канала h = 0,1 м, L₀ = 0,1 м, L₂ = 0,2 м.

 

Р и с.  1.  Общая схема моделируемого процесса
F i g.  1.  General scheme of the simulated process

 

Источник: Рисунок 1 составлен авторами статьи.
Source: figure 1 is compiled by the authors of the article.

Примечание: u₀ – продольная скорость газа и пылевой фракции, м/с; v₀ – продольная скорость поперечного вдува газа и капельных фракций, м/с; y – поперечная координата, м; x – продольная координата, м; L₀ – правая продольная координата поверхности вдува, м; L₁ – левая продольная координата поверхности вдува, м; φ – угол вдува, радианы.
Note: u₀ is the longitudinal velocity of gas and dust fraction; v₀ is the longitudinal velocity of transverse injection of gas and droplet fractions; y is the transverse coordinate; x is the longitudinal coordinate; L₀ is the right longitudinal coordinate of the injection surface; L₁ is the left longitudinal coordinate of the injection surface; φ is the injection angle.

Размеры ячеек вдоль продольной и поперечной координат соответственно Δx = 0,002, Δy = 0,001 м.

Численные расчеты вектора скорости несущей среды проводились в рамках решения системы уравнений Навье – Стокса с однородными граничными условиями Дирихле на стенках канала, для модуля скорости несущей среды $\left|V_1\right|=\sqrt{u_1^2+v_1^2}$ (рис. 2) можно наблюдать «параболический» ламинарный профиль течения вязкой среды в канале, при котором максимальные значения модуля скорости несущей среды достигаются вблизи оси симметрии канала¹⁰.

 

Р и с.  2.  Модуль скорости несущей среды
F i g.  2.  Velocity modulus of the carrier medium

 

Источник: Рисунки 2, 3 составлены авторами статьи с помощью программы Surfer.
Source: Figures 2 and 3 are made by the authors of the article using the program Surfer.

Примечание: |V₁| – модуль скорости несущей среды, м/с; x – продольная координата, м; y – поперечная координат, м.
Note: |V₁| is the velocity module of the carrier medium, м/с; x is the longitudinal coordinate, m; y is the transverse coordinate, m.

 

Пылевая фракция с размером частиц d₁ = 2 мкм имеет физическую плотность материала частиц – ρ₂₀ = 2 500 кг/м³, начальное объемное содержание – α₂₀ = 0,00004. Через боковую поверхность канала втекают четыре капельных фракции с размерами частиц d₂ = 4 мкм, d₃ = 8 мкм, d₄ = 20 мкм, d₅ = 40 мкм и плотностью материала капель – ρ_i0 = 1 000 кг/м³. Предполагалось, что у всех четырех капельных фракций вблизи поверхности вдува одинаковое постоянное объемное содержание – α_i0 = 25·10⁻⁶, i = 3,…,6.

Численные расчеты демонстрируют, что в процессе движения многофракционной газовзвеси в канале за счет коагуляции частиц происходит поглощение пылевой фракции капельными фракциями (рис. 3).

 

Р и с.  3.  Пространственное распределение средней плотности материала пылевой фракции

F i g.  3.  Spatial distribution of the average density of the dust fraction material

На рисунке 4 представлено пространственное распределение средней плотности пылевой фракции вдоль оси х (у = h/2), при различных углах вдува капельной фракции газовзвеси в поперечном распределении пылевой фракции. Наименьшее значение средней плотности достигается когда угол вдува составляет – φ = π/2: ρ₂ = 0,0695 кг/м³. Для углов φ = π/6 и φ = 5π/6 величины средней плотности составляют – ρ₂ = 0,0714 кг/м³, ρ₂ = 0,0708 кг/м³ соответственно. Для углов φ = π/4 и φ = 3π/4 величины средней плотности составляют – ρ₂ = 0,0707 кг/м³ и ρ₂ = 0,0702 кг/м³ соответственно. Для углов φ = π/3 и φ = 5π/6 величины средней плотности составляют – ρ₂ = 0,0701 кг/м³ и ρ₂ = 0,0696 кг/м³ соответственно. При втекании капельных фракций против движения потока средняя плотность запыленной среды уменьшается более интенсивно.

 

Р и с.  4.  Продольное распределение средней плотности  материала пылевой фракции, в момент времени t = 0,0031 с
F i g.  4.  Longitudinal distribution of the average density  of the dust fraction material at t =0,0031 s

Источник: графики для рисунков 2–10 построены авторами с помощью программы Origin 2022.
Source: The graphs for Figures 2–10 are compiled  by the authors using the program Origin 2022.

 

На рисунке 5 показано распределение средней плотности пылевой фракции газовзвеси вдоль оси у (х = L/2) канала при различных углах втекания капельных фракций, наименьшее значение средней плотности пылевой фракции наблюдается вблизи оси симметрии канала. Минимальное значение средней плотности достигается для угла φ = π/2. Значение средней плотности для углов φ и π – φ близки.

Р и с.  5.  Поперечное распределение средней плотности  материала пылевой фракции, момент времени t = 0,0031 с
F i g.  5.  Transverse distribution of the average density  of the dust fraction material, time t = 0,0031 s

 

На рисунке 6 представлен отрезок временной зависимости объемного содержания пылевой фракции в точке х = L/2, у = h/2. Наиболее интенсивно убывание объемного содержание пылевой фракции происходит, если угол между потоком пылевой фракции и втекающими капельными фракциями – φ = π/2, наименее интенсивно убывание происходит при втекании капельных фракций по направлению движения запыленного потока с углом – φ = π/6. В точке (x = 0,5h, y = 0,5L)  φ = π/6 – α₂ = 0,21625α₂₀, φ = π/4 – α₂ = 0,2095α₂₀, φ = π/3 – α₂ = 0,2035α₂₀,  φ = π/2 – α₂ = 0,2α₂₀, φ = 2π/3 – α₂ = 0,2175α₂₀, φ = 3π/4 – α₂ = 0,20475α₂₀, φ = 5π/6 – α₂ = 0,21125α₂₀ в момент времени t = 0,07 c. Интенсивность убывания объемного содержания пылевой фракции для углов φ и π – φ близки, но для случая тупого угла интенсивность убывания больше.

Результаты численных расчетов демонстрируют, что угол вдува газокапельной смеси – φ оказывает влияние на линии тока несущей среды. При остром угле вдува – φ = π/6 (рис. 7 a), линии тока направлены по потоку, разворота линий тока не наблюдается. При этом за счет разности скоростей вдуваемого и основного потока происходит уменьшение скорости движения всей смеси. При вдуве газа под углом – φ = π/2 (рис. 7 b) и тупым углом – φ = 5π/6 (рис. 7 c) наблюдаются отличия линий тока газа. Для тупого угла (рис. 7 c) наблюдается разворот линий тока газа, при этом происходит уменьшение скорости движения несущей среды, связанное с тем, что вдув происходит против движения основного потока. Для углов вдува φ = π/6, φ = π/4, φ = π/3, φ = π/2, φ = 2π/3, φ = 3π/4, φ = 5π/6 максимальные значения модуля скорости несущей среды – max|V₁| в поперечном сечении х = L/2, момент времени t = 0,0031 с соответственно – max|V₁| = 25,5 м/с, max|V₁| = 26,5 м/с, max|V₁| = 27,3 м/с, max|V₁| = 28,22 м/с, max|V₁| = 27,93 м/с, max|V₁| = 27,3 м/с, max|V₁| = 26,5 м/с соответственно.

Р и с.  6.  Временная зависимость объемного содержания в точке х = L/2, у = h/2
F i g.  6.  Time dependence of volume content at point x = L/2, y = h/2

 

Р и с.  7.  Линии тока несущей среды при вдуве капельных фракций:
a) под углом φ = π/6; b) под углом φ = π/2; c) под углом φ = 5π/6
F i g.  7.  Streamlines of the carrier medium during injection of droplet fractions:
a) at an angle φ = π/6; b) at an angle φ = π/2; с) at an angle of φ = 5π/6

 

Максимальное значение модуля скорости несущей среды достигается для вдува капельных фракций поперек канала, угол вдува – φ = π/2.

Поперечные распределения модуля разности скоростей для пылевой фракции и капельной фракции с диаметром дисперсных включений d₄ = 20 мкм (рис. 8) демонстрирует, что наибольшее значение модуля разности скорости пылевой фракции и фракции частиц с дисперсностью d = 20 мкм достигается для угла вдува φ = π/2. При прочих углах втекания капельной фракции наблюдается меньшее значение скоростного скольжения.

 

Р и с.  8.  Пространственное распределение вдоль оси у модуля разности скоростей  фракций для различных углов вдува
F i g.  8.  Spatial distribution along the y-axis of the difference in fraction velocities  for different injection angles

 

В таблице представлены максимальные значения модуля разности скоростей пылевой фракции и капельных фракций для поперечного сечения при координате х = 0,5L для разных углов втекания капельных фракций.

 

Таблица Влияние угла вдува капельных фракций на величину максимального скоростного скольжения пылевой фракции и различных капельных фракций
Table The influence of the injection angle of droplet fractions on the magnitude of the maximum velocity slip of the dust fraction and various droplet fractions

Угол вдува, φ / injection angle, φ	max|V3 – V2|, м/с при d2 = 4 мкм / max|V3 – V2|, m/s at d2 = 4 μm	max|V4 – V2|, м/с при d3 = 8 мкм / max|V4 – V2|, m/s at d3 = 8 μm	max|V5 – V2|, м/с при d4 = 20 мкм / max|V5 – V2|, m/s at d4 = 20 μm	max|V6 – V2|, м/с при d5 = 40 мкм /  max|V6 – V2|, m/s  at d5 = 40 μm
π/6	0,91	3,50	11,36	19,30
π/4	0,94	3,71	11,58	19,50
π/3	0,96	3,80	11,70	19,70
π/2	1,02	3,95	12,00	20,00
2π/3	0,97	3,85	11,88	19,85
3π/4	0,95	3,74	11,75	19,70
5π/6	0,92	3,55	11,50	19,50

 

Из таблицы следует, что наибольшее значение модуля разности скоростей пылевой фракции и капельных фракций различных размеров наблюдается для угла φ = π/2. Для углов π – φ (π/6 ≤ φ ≤ π/3), когда вдув осуществляется против потока запыленной среды, интенсивность скоростного скольжения пылевой фракции и капельных фракций имеет большее значение, чем для углов φ (π/6 ≤ φ ≤ π/3), вдува по направлению движения запыленной среды.

 

ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ

Работа посвящена вопросам коагуляции многофракционной взвеси в потоке газа. Исследовалось влияние угла вдува капельных фракций на распределение средней плотности пылевой фракции. В отличие от известных в научной литературе результатов для описания процесса коагуляции применялась континуальная Эйлерова математическая модель. Проведены расчеты для углов вдува потока меньших и больших π/2. Выявлено, что угол вдува капельных фракций оказывает влияние на интенсивность коагуляции дисперсных включений. Наиболее интенсивное убывание средней плотности пылевой фракции наблюдается для угла φ = π/2. Для углов вдува газокапельного потока φ и π–φ распределения объемных содержаний пылевой фракции близки. Для вдува против потока φ > π/2 интенсивность убывания объемного содержания пылевой фракции имеет большее значение, чем при вдуве по направлению потока – φ < π/2. Закономерность можно объяснить тем, что для капельных фракций, имеющих размеры большие, чем размеры дисперсных включений пылевой фракции, наибольшее значение скоростного скольжения с пылевой фракцией достигается для угла – φ = π/2. Минимизация остаточной концентрации может быть достигнута выбором направления вдува капельных фракций и исключением в спектре размеров фракций с малым скоростным скольжением относительно пылевой фракции. При этом играет роль также и концентрация распыляемых фракций. Таким образом, задача оптимизации является многофакторной. В данном исследовании рассматривается только выбор направления дисперсного капельного потока, при котором наблюдается повышенная интенсивность коагуляции пылевой и капельных фракций. В расчетах выявлено, что для широкого диапазона размера капельных фракций наибольшая величина скоростного скольжения наблюдается для вдува капельного потока перпендикулярно направлению потока запыленной среды. Ограничением модели является то, что в исследовании не учитывалось влияние турбулентной вязкости на динамику несущей среды и фракций дисперсной фазы, что имело бы значение для скоростных газодисперсных потоков. Полученные результаты можно использовать при оптимизации аппаратов жидкостной очистки запыленных сред.

 

¹ Нигматулин Р.И. Основы механики гетерогенных сред. М.: Наука; 1978. 336 с.

² Дейч М.Е., Филиппов Г.А. Газодинамика двухфазных сред. М.: Энергоиздат; 1981. 472 с.

³ Киселев C.П., Руев Г.А., Трунев А.П., Фомин В.М., Шавалеев М.Ш. Ударно-волновые процессы в двухкомпонентных и двухфазных средах. Новосибирск: Наука; 1992. 261с.

⁴ Кутушев А.Г. Математическое моделирование волновых процессов в аэродисперсных и порошкообразных средах. Санкт-Петербург: Недра; 2003. 284 с.; Федоров А.В., Фомин В.М., Хмель Т.А. Волновые процессы в газовзвесях частиц металлов. Новосибирск: Параллель; 2015. 301 c.

⁵ Алемасов В.Е., Дрегалин А.Ф., Тишин А.П., Худяков В.А. Термодинамические и теплофизические свойства продуктов сгорания: Методы расчета. М.: ВИНИТИ; 1971. 267 с.

⁶ Нигматулин Р.И. Основы механики гетерогенных сред. М.: Наука; 1978. 336 с.

⁷ Алемасов В.Е., Дрегалин А.Ф., Тишин А.П., Худяков В.А. Термодинамические и теплофизические свойства продуктов сгорания: Методы расчета. М.: ВИНИТИ; 1971. 267 с.

⁸ Флетчер К. Вычислительные методы в динамике жидкостей. М.: Мир; 1991. 551 с.

⁹ Там же.

¹⁰ Флетчер К. Вычислительные методы в динамике жидкостей. М.: Мир;1991. 551 с.

 

About the authors

Dmitry A. Tukmakov

Federal State Budgetary Institution of Science “Kazan Scientific Center of Russian Academy of Sciences”

Email: tukmakovda@imm.knc.ru
ORCID iD: 0000-0002-0335-8548
SPIN-code: 3556-8576
Scopus Author ID: 55776164300
ResearcherId: K-6563-2014

Cand.Sci. (Phys.-Math.), senior researcher fellow of Institute of Mechanics and Engineering

2 Lobachevsky St., Kazan 420100, Russian Federation

Aleksei L. Tukmakov

Federal State Budgetary Institution of Science “Kazan Scientific Center of Russian Academy of Sciences”

Author for correspondence.
Email: tukmakov@imm.knc.ru
ORCID iD: 0000-0002-8570-4140

Dr.Sci. (Phys.-Math.), Leading Researcher of Institute of Mechanics and Engineering

2 Lobachevsky St., Kazan 420100, Russian Federation

References

Supplementary files