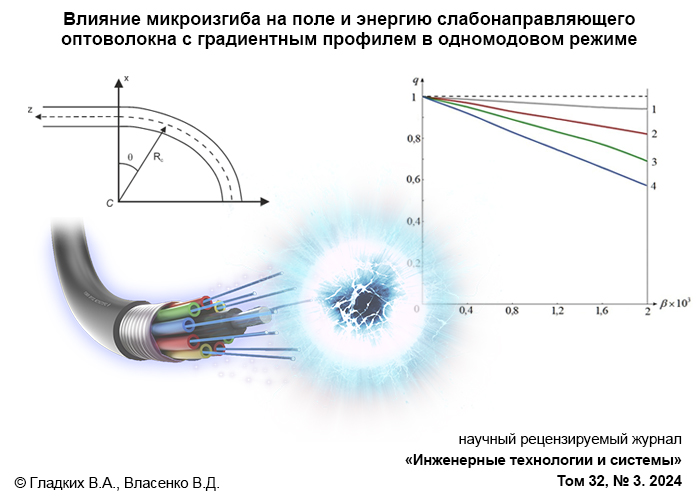
Micro-Bending Effect on the Field and Energy of Weakly Guiding Optical Fiber with a Gradient Profile in Single-Mode Regime

Texto integral

Введение

При изгибе оптического волокна появляются дополнительные потери энергии, быстро растущие после достижения определенного критического радиуса изгиба. Этот критический радиус может быть очень мал (всего несколько мм) у волокон с высокой числовой апертурой, тогда как допустимый радиус изгиба гораздо больше (часто десятки см) для волокон в одномодовом режиме с большой площадью поперечной моды.

Даже при отсутствии макроскопических изгибов волокна могут быть потери, вызванные микроизгибами, то есть микроскопическими неровностями (нарушениями структуры) в волокне.

Замечено, что изгибы являются также причиной уменьшения эффективной площади поперечной моды. Это особенно заметно у волокон со ступенчатым профилем, которые имеют большую площадь поперечной моды. Также изгибы вызывает двойное лучепреломление.

Нарушение требования минимального радиуса изгиба может привести к ухудшению рабочих свойств кабеля. Радиус изгиба оптического кабеля оказывает влияние на радиус изгиба оптического волокна, находящегося непосредственно внутри кабеля. При соблюдении минимального радиуса изгиба оптического волокна не нарушается принцип передачи оптического сигнала: эффект полного внутреннего отражения сохраняется, сигнал без лишнего затухания передается по оптическим волокнам. Когда минимальный радиус изгиба оптического волокна не соблюдается, на месте изгиба возникает макроизгиб, при котором свет выходит за пределы сердцевины волокна и затухает. Излишнее затухание в линии недопустимо, поэтому соблюдение минимально допустимого радиуса изгиба кабеля является обязательным условием при эксплуатации волоконно-оптической линии связи.

Целью работы является исследование зависимости энергии внутри волокна от радиуса изгиба слабонаправляющего оптоволокна с градиентным профилем показателя преломления в одномодовом режиме с различными значениями волноводного параметра при малых изгибах.

Обзор литературы

В классических монографиях А. Снайдера, Дж. Лава¹ и Х. Г. Унгера² представлена обширная информация о различных видах волноводов с кратким описанием как экспериментальных и теоретических результатов с большим количеством примеров, так и различных математических методов. Однако прошло немало времени с момента издания этих трудов. Исследование данной тематики значительно продвинулось. Отметим кратко некоторые направления.

В монографии K. Okamoto³ доказано, что искривление одномодового оптического волокна приводит к двум основным формам дополнительных потерь при передаче: переходные потери и чистые потери на изгибе. Переходные потери и связанное с ними лучевое излучение, которое наблюдается в начале изгиба, могут быть объяснены с помощью модифицированной теории связанных мод [1]. Проблема потерь в волоконных световодах на изгибах малого радиуса возникла с их появлением. Одним из методов теоретического решения этой проблемы является метод конформного отображения изогнутого световода в прямолинейный с перекошенным профилем показателя преломления [2–4].

В работах [5; 6] предложен механизм полезный для настройки профиля поля в одномодовых оптических волокнах, предполагающий локальный и постоянный изгиб волокна с радиусом изгиба в несколько сотен мкм. В публикациях [7–9] представлен новый подход к разработке оптических волокон с градиентным профилем. В статье [10] рассмотрен круглый в поперечном сечении регулярный слабопроводящий волоконный световод с двойной оболочкой. Для одномодового режима такого волновода получено выражение, которое может дать оценку части мощности поля моды, проникающей во внешнюю сплошную оболочку, в стандартном подходе и в Гауссовой модели.

Новый и простой подход к разработке двумерного датчика смещения, основанный на потерях в макроизгибе и эффекте связи оптической мощности, представлен в работах [11–13]. В статье [14] рассмотрена проблема улучшения технических характеристик волоконно-оптических измерительных преобразователей, определяемых механической надежностью изогнутого оптического волокна. Установлена зависимость интенсивности светового потока от изменения радиуса изгиба оптического волокна. В статье [15] для степенного профиля с произвольным показателем степени в первом приближении методом функции Грина получено выражение для поля внутри градиентного волокна в одномодовом режиме.

Подходы к разработке оптических волокон и потери на изгибах исследованы в работах [16–18]. В статье [19] рассмотрен математический аппарат, позволяющий сформировать критерии качественной и количественной оценки несанкционированного доступа к построенным волоконно-оптическим линиям связи (ВОЛС) на основе определения показателей эффективности отвода оптического излучения из волоконных световодов. Один из простейших и очевидных методов «съема» информации можно осуществить путем отведения мощности оптического излучения из ВОЛС за счет макроизгиба его волоконных световодов.

В работе [20] численно и экспериментально исследовано расщепление линий резонатора Фабри-Перо, образованного участком стандартного изогнутого одномодового волоконного световода с металлизированными торцами. Публикация [21] посвящена характеристике профиля пучка, выходящего из оптического волокна с двойной оболочкой и имеющего разную геометрию сечения. В работе [22] рассмотрен слабонаправляющий градиентный световод в одномодовом режиме, решено уравнение для электрического поля в сердцевине световода в общем виде в первом приближении.

Волоконная брэгговская решетка представляет собой широко используемую чувствительную структуру оптического волокна. В работе [23] представлена простая структура, состоящая из обычного одномодового волокна и секции многомодового волокна с волоконной брэгговской решеткой. Она может одновременно осуществлять двухпараметрическое измерение микроизгиба и температуры. Различные аспекты оптических потерь на изгибах световодов подробно описаны в работах [24–26]. В публикациях [27–29] рассмотрен новый подход к моделированию оптического волокна. В обзоре [30] представлены результаты системного анализа существующих рекомендаций по волоконным световодам. Проведена систематизация физических параметров и эксплуатационных характеристик стандартизированных волоконных световодов.

Обеспечение малых потерь на границе соединения волокна с полой сердцевиной и традиционного волокна с твердой сердцевиной имеет большое значение для многих практических применений волокон с твердой сердцевиной. В работе [31] с помощью моста в виде волокна с градиентом показателя преломления исследуется высокотемпературное соединение оптических волокон двух типов – антирезонансного волокна с полой сердцевиной и волокна с твердой сердцевиной, обеспечивающих малые потери при прохождении лазерного излучения.

Пучки или жгуты оптических волокон находят все больше применений в различных областях волоконной оптики, несмотря на сравнительно низкое разрешение подобных устройств. Одним из способов решения указанной проблемы является использование материалов с высоким показателем преломления, что позволит добиться сильной локализации мод излучения в волокне. В обзоре [32] представлен способ применения для этих целей сапфировых волокон с высоким показателем преломления n > 3.

Волоконная оптика как научное направление начала активно развиваться с момента разработки технологии волоконных световодов. Научный интерес к изгибу оптововолокна возник практически вместе с появлением самих световодов. Изгиб оптического волокна является важным инструментом научных исследований в лазерной физике, оптической связи, технике обработки информации, оптических вычислительных машинах, оптических датчиках различных физических вели-
чин и т. д. Основываясь на анализе рассмотренных публикаций, делаем вывод, что большинство вопросов, связанных с изгибами оптического волокна, изучены недостаточно полно и требуют дополнительных исследований и экспериментов.

Материалы и методы

Пусть $\overrightarrow{E}$ – электрическое поле прямого поляризованного участка по оси х слабонаправляющего световода с постоянной распространения основной моды β:

${\overrightarrow{E}}_{str}\left(t,x,y,z\right)={\overrightarrow{e}}_x\exp \left(-i\omega t\right)\exp \left(i\beta z\right)A_{str}\left(r\right).$     (1)

Здесь ось z направлена вдоль оси световода; (x; y) – координаты поперечного сечения; ω – циклическая частота; ${\overrightarrow{e}}_x$ – единичный вектор вдоль оси x; A_str(r) – координатная часть электрического поля прямолинейного участка световода, где $r=\sqrt{x^2+y^2}$.

Согласно уравнениям Максвелла для диэлектрических прозрачных сред, A_str(r) удовлетворяет дифференциальному уравнению в декартовых координатах:

$\left({\partial }^2/\partial x^2+{\partial }^2/\partial y^2+\left[k^2{n}^2\left(r\right)-{\beta }^2\right]\right)A_{str}\left(r\right)=0$ ,                          (2)

где k = ω/c; с – скорость света; n²(r) – показатель преломления волоконного световода, который обычно записывается в виде:

$\begin{array}{c}{n}^2\left(r\right)=\left\{\begin{array}{l}{n}_{co}^2\left[1-2\Delta h\left(r\right)\right]=n_{co}^2-{\left(V/k\rho \right)}^{2}h\left(r\right),0\le r\le \rho ,h\left(0\right)\equiv \mathrm{0,}h\left(\rho \right)=\mathrm{1,}\\ n_{cl}^2,r>\rho ,\end{array}\right.\\ 2\Delta \equiv \left(n_{co}^2-n_{cl}^2\right)/n_{co}^2\equiv {\left(NA\right)}^2/n_{co}^2,V\equiv k\rho NA.\end{array}$       (3)

Здесь Δ – высота профиля; NA – числовая апертура; V – волноводный параметр; h(r) – функция, принимающая значения от 0 до 1 при изменении r от 0 до ρ.

С учетом (3) запишем уравнение (2) в виде:

 $\left.\left\{{\partial }^2/\partial x^2\right.+{\partial }^2/\partial y^2+{\chi }_1^2\right\}{A}_{str}\left(r\right)=-4\pi F_{str}\left(r\right),$               (4)

 ${\chi }_1^2\equiv k^2{n}_{co}^2-{\beta }^2,F_{str}\left(r\right)\equiv -\frac{V^2}{4\pi {\rho }^2}h\left(r\right)A_{str}\left(r\right),$ где 0 ≤ r ≤ ρ.

Рассмотрим однородное уравнение, соответствующее уравнению (4), и перейдем к полярным координатам, для основной моды получим:

$\begin{array}{c}\left.\left\{{\partial }^2/\partial x^2\right.+{\partial }^2/\partial y^2+{\chi }_1^2\right\}{A}_{str(0)}\left(r\right)\equiv \mathrm{0,}\\ \left\{d^2/d{r}^2+\left(1/r\right)d/dr+{\chi }_1^2\right\}{A}_{str(0)}=\mathrm{0,}\\ A_{str(0)}\left(r\right)=J_0\left({\chi }_{1}r\right),\end{array}$

где J₀(χ₁r) – функция Бесселя нулевого порядка. Таким образом, общее решение уравнения (4) для прямого участка световода можно записать в виде:

 $A_{str\left(tot\right)}\left(r\right)=\mathrm{const}\cdot \left\{J_0\left({\chi }_{1}r\right)+A_{str}\left(r\right)\right\},0\le r\le \rho ,$                    (5)

где A_str(r) – частное решение неоднородного уравнения (4).

В случае изогнутого участка световода пусть θ – угловая координата по изгибу, отчитываемая от оси x; R_c – радиус кривизны с центром в точке C вне волновода, постоянный относительно оси изгиба; z – расстояние вдоль изогнутого участка (рис. 1). Пунктирная линия – ось волновода, ось y направлена перпендикулярно плоскости рисунка.

 

Рис. 1. Схематическое изображение волоконного световода с профилем показателя преломления n(r), изогнутого в виде дуги с постоянным радиусом R_c  и угловой координатой по изгибу θ (пунктирная линия проходит по оси световода)

Fig. 1. Schematic representation of a fiber-optic light guide with a refractive index profile n(r), bent in the form of an arc with a constant radius R_с and angular coordinate along the bend θ (the dotted line runs along the axis of the fiber-optic light guide)

Источник: составлено автором.

Source: the diagram was drawn up by the authors of the article.

На изгибе поле должно иметь угловую зависимость вида exp(iκθ), где κ – пунктирная постоянная, подлежащая определению. Установим локальную постоянную распространения $\stackrel{\wedge }{\beta }$  соотношением:

 $\exp \left(i\kappa \theta \right)\equiv \exp \left(i\stackrel{\wedge }{\beta }z\right),{\left.z\right|}_{\theta =0}=0.$                     (6)

Вводя полярные координаты в поперечном сечении, согласно рисунку 1 и учитывая соотношение (6), запишем:

$z=\left(R_c+r\cos \phi \right)\theta \to \kappa =\stackrel{\wedge }{\beta }\left(R_c+r\cos \phi \right).$                       (7)

Поскольку на оси световода (r = 0) в начале изгиба должно быть $\stackrel{\wedge }{\beta }=\beta$, то для постоянной κ находим κ = βR_c и из предыдущего соотношения получаем:

$\begin{array}{c}\beta R_C=\stackrel{\wedge }{\beta }(R_C+r\cos \phi ),\\ \stackrel{\wedge }{\beta }=\frac{\beta R_C}{(R_C+r\cos \phi )}\approx (r<<R_C)\approx \beta \left\{1-\frac{r}{R_C}\cos \phi \right\}.\end{array}$

Для слабонаправляющего световода:

$\stackrel{\wedge }{{\beta }^2}\approx {\beta }^2\left(1-2\frac{r}{R_c}\cos \phi \right)\approx {\beta }^2-2\underset{¯}{{\beta }^2}\frac{r}{R_c}\cos \phi \approx {\beta }^2-2\underset{¯}{k^2{n}_{co}^2}\frac{r}{R_c}\cos \phi .$ (8)

Таким образом, заменяя изогнутый участок на эквивалентный прямой с заменой β на локальную постоянную распространения $\stackrel{\wedge }{\beta }$, аналогично (1) запишем:

$E_{curv}\left(t,x,y,z\right)=\text{exp}\left(-i\omega t\right)\text{exp}\left(i\stackrel{\wedge }{\beta }z\right)A_{curv}\left(r\right)$,

где A_curv(r) – координатная часть электрического поля изогнутого участка световода.

Для A_curv(r) аналогично (4) и с учетом (9) получим:

$\left.\left\{{\partial }^2/\partial x^2\right.+{\partial }^2/\partial y^2+{\chi }_1^2\right\}{A}_{curv}\left(r\right)=-4\pi Q_{curv}\left(r\right),$ (9)

где ${\chi }_1^2\equiv k^2{n}_{co}^2-{\beta }^2,Q_{curv}\left(r\right)\equiv F_{curv}\left(r\right)+f_{curv}\left(r\right),F_{curv}\left(r\right)\equiv -\frac{V^2}{4\pi {\rho }^2}h\left(r\right)A_{curv}\left(r\right),$ $f_{curv}\left(r\right)\equiv \frac{k^2{n}_{co}^2}{2\pi }\frac{r}{R_c}\cos \phi A_{curv}\left(r\right).$

Аналогично (5) общее решение уравнения (9) для изогнутого участка световода можно записать в виде:

$A_{curv\left(tot\right)}\left(r\right)=\mathrm{const}\cdot \left\{J_0\left({\chi }_{1}r\right)+A_{cerv}\left(r\right)\right\},0\le r\le \rho ,$ (10)

где A_curv(r) – частное решение неоднородного уравнения (9).

Результаты исследования

Частные решения неоднородных уравнений типа (4) и (7) проще искать методом Грина $G\left(x,y;x^{\prime },y^{\prime }\right)$  [33]:

$\begin{array}{c}\left({\partial }^2/\partial x^2+{\partial }^2/\partial y^2+{\chi }_1^2\right)X\left(x,y\right)=-4\pi Z\left(x.y\right),\\ X\left(x,y\right)={\displaystyle \iint d{x}^{\prime }d{y}^{\prime }G\left(x,y;x^{\prime },y^{\prime }\right)}Z\left(x^{\prime },y^{\prime }\right),\\ G\left(x,y;x^{\prime },y^{\prime }\right)=i\pi H_0^{\left(1\right)}\left({\chi }_1{r}_{12}\right),\\ r_{12}=\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2},\end{array}$ (11)

где $H_0^{\left(1\right)}\left(x\right)$ – функция Ханкеля первого рода нулевого порядка от аргумента x. Переходя к полярным координатам и воспользовавшись частным случаем «теоремы сложения» для цилиндрических функций⁴:

$H_0^{\left(1\right)}\left({\chi }_1{r}_{12}\right)=H_0^{\left(1\right)}\left({\chi }_{1}r\right)J_0\left({\chi }_1{r}^{\prime }\right)+2{\displaystyle \sum _{k=1}^{\infty }{H}_k^{\left(1\right)}\left({\chi }_{1}r\right)J_k\left({\chi }_1{r}^{\prime }\right)\cos \left(k{\phi }^{\prime }\right)}$ ,

с помощью формул для уравнений (4) и (9) соответственно, запишем решения в виде:

$A_{str}\left(r\right)=-\frac{i\pi V^2}{2{\rho }^2}{H}_0^{\left(1\right)}\left({\chi }_{1}r\right){\displaystyle \underset{0}{\overset{\rho }{\int }}{r}^{\prime }{J}_0\left({\chi }_1{r}^{\prime }\right)h\left(r^{\prime }\right)A_{str}\left(r^{\prime }\right)}d{r}^{\prime }$ (12)

и

$\begin{array}{l}{A}_{curv}\left(r\right)=-\frac{i\pi V^2}{2{\rho }^2}{H}_0^{\left(1\right)}\left({\chi }_{1}r\right){\displaystyle \underset{0}{\overset{\rho }{\int }}d{r}^{\prime }{r}^{\prime }{J}_0\left({\chi }_1{r}^{\prime }\right)h\left(r^{\prime }\right)A_{curv}\left(r^{\prime }\right)}+\\ +\frac{i\pi k^2{n}_{co}^2}{R_c}{H}_1^{\left(1\right)}\left({\chi }_{1}r\right){\displaystyle \underset{0}{\overset{\rho }{\int }}d{r}^{\prime }{r^{\prime }}^2{J}_1\left({\chi }_1{r}^{\prime }\right)A_{curv}\left(r^{\prime }\right)},\end{array}$ (13)

где $H_k^{\left(1\right)}\left(x\right)$ – функция Ханкеля первого рода k-го порядка; J_k(x) – функция Бесселя k-го порядка.

Согласно выражениям (12–13) для (5) и (10) в первом приближении запишем для общих решений:

$\begin{array}{l}{A}_{str\left(tot\right)}\left(\gamma \right)\approx \mathrm{const}\cdot \left\{J_0\left({\chi }_1\rho \gamma \right)-\frac{i\pi V^2}{2}{H}_0^{\left(1\right)}\left({\chi }_1\rho \gamma \right)\Theta \left({\chi }_1\rho \right)\right\},\\ \Theta \left({\chi }_1\rho \right)\equiv {\displaystyle \underset{0}{\overset{1}{\int }}\gamma J_0^2\left({\chi }_1\rho \gamma \right)h\left(\gamma \right)d\gamma },\gamma \equiv \frac{r}{\rho }\end{array}$                          (14)

и

$\begin{array}{l}{A}_{curv\left(tot\right)}\left(\gamma \right)\approx \left\{{\left(k\rho \right)}^2{n}_{co}^2=\frac{V^2}{2\Delta }\right\}\approx \\ \approx \text{const}\cdot \left\{J_0\left({\chi }_1\rho \gamma \right)-\frac{i\pi V^2}{2}{H}_0^{\left(1\right)}\left({\chi }_1\rho \gamma \right)\Theta \left({\chi }_1\rho \right)+\right.\\ \left.+i\pi \frac{V^2}{2\Delta }\frac{\rho }{R_c}{H}_1^{\left(1\right)}\left({\chi }_1\rho \gamma \right){\displaystyle \underset{0}{\overset{1}{\int }}{\gamma }^2{J}_0\left({\chi }_1\rho \gamma \right)J_1\left({\chi }_1\rho \gamma \right)d\gamma }\right\}.\end{array}$

В уравнении (5) $A_{str\left(0\right)}\left(r\right)=J_0\left({\chi }_{1}r\right)$ и аналогичным с ним образом в выражении (10) $A_{curv\left(0\right)}\left(r\right)=A_{str\left(0\right)}\left(r\right)=J_0\left({\chi }_{1}r\right)$.

Согласно данным технического руководства, для оптоволокон 2D Î (0,006; 0,060), поэтому для простоты расчетов из этого интервала выберем 2D » 0,010 ® D » 0,005. Таким образом, формула принимает вид:

$\begin{array}{l}{A}_{curv\left(tot\right)}\left(\gamma \right)\approx \mathrm{const}\cdot \left\{J_0\left({\chi }_1\rho \gamma \right)-\frac{i\pi V^2}{2}{H}_0^{\left(1\right)}\left({\chi }_1\rho \gamma \right)\Theta \left({\chi }_1\rho \right)+\right.\\ \left.+i\pi {10}^2{V}^2\frac{\rho }{R_c}{H}_1^{\left(1\right)}\left({\chi }_1\rho \gamma \right){\displaystyle \underset{0}{\overset{1}{\int }}{\gamma }^2{J}_0\left({\chi }_1\rho \gamma \right)J_1\left({\chi }_1\rho \gamma \right)d\gamma }\right\}.\end{array}$

Поскольку функция Ханкеля первого рода порядка k имеет вид $H_k^{\left(1\right)}\left(z\right)=J_k\left(z\right)+i{N}_k\left(z\right)$, где $J_k\left(z\right),N_k\left(z\right)$  – соответственно функция Бесселя и функция Неймана порядка k, перепишем выражения (12‒13) в следующем виде для удобства дальнейших расчетов:

$\begin{array}{l}{A}_{str\left(tot\right)}\left(\gamma \right)=\mathrm{const}\cdot \left\{a_1\left(\gamma \right)-i{b}_1\left(\gamma \right)\right\},\\ a_1\left(\gamma \right)\equiv J_0\left({\chi }_1\rho \gamma \right)+\frac{\pi V^2}{2}{N}_0\left({\chi }_1\rho \gamma \right)\Theta \left({\chi }_1\rho \right),\\ b_1\left(\gamma \right)\equiv \frac{\pi V^2}{2}{J}_0\left({\chi }_1\rho \gamma \right)\Theta \left({\chi }_1\rho \right)\end{array}$               (15)

и

 $\begin{array}{l}{A}_{curv}\left(\gamma \right)=\mathrm{const}\cdot \left\{\left(a_1\left(\gamma \right)-a_2\left(\gamma \right)\right)-i\left(b_1\left(\gamma \right)-b_2\left(\gamma \right)\right)\right\},\\ a_2\equiv {10}^2\pi V^2\frac{\rho }{R_c}{N}_1\left({\chi }_1\rho \gamma \right)\Psi \left({\chi }_1\rho \right),\\ b_2\left(\gamma \right)={10}^2\pi V^2\frac{\rho }{R_c}{J}_1\left({\chi }_1\rho \gamma \right)\Psi \left({\chi }_1\rho \right),\Psi \left({\chi }_1\rho \right)\equiv \underset{0}{\overset{1}{\int }}{\gamma }^2{J}_0\left({\chi }_1\rho \gamma \right)J_1\left({\chi }_1\rho \gamma \right)d\gamma .\end{array}$          (16)

Учитывая выражения (15‒16), определим величину q (отношение энергии W_curv изогнутого участка волокна к энергии W_str прямого участка волокна):

$\begin{array}{l}q\equiv \frac{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|A_{curv}\left(\gamma \right)\right|}^2\gamma d\gamma }}{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|A_{str}\left(\gamma \right)\right|}^2\gamma d\gamma }}=\\ =1-\frac{2{\displaystyle \underset{0}{\overset{1}{\int }}{a}_1\left(\gamma \right)a_2\left(\gamma \right)\gamma d\gamma }+2{\displaystyle \underset{0}{\overset{1}{\int }}{b}_1\left(\gamma \right)b_2\left(\gamma \right)\gamma d\gamma }-{\displaystyle \underset{0}{\overset{1}{\int }}{a}_2^2\left(\gamma \right)}\gamma d\gamma -{\displaystyle \underset{0}{\overset{1}{\int }}{b}_2^2\left(\gamma \right)\gamma d\gamma }}{{\displaystyle \underset{0}{\overset{1}{\int }}{a}_1^2\left(\gamma \right)\gamma d\gamma }+{\displaystyle \underset{0}{\overset{1}{\int }}{b}_1^2\left(\gamma \right)\gamma d\gamma }},\end{array}$  (17)

где

$\begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}{a}_2^2\left(\gamma \right)\gamma d\gamma }={10}^4{\pi }^2{V}^4{\left(\frac{\rho }{R_c}\right)}^2{\Psi }^2\left({\chi }_1\rho \right)I_1;\\ {\displaystyle \underset{0}{\overset{1}{\int }}{b}_2^2\left(\gamma \right)}\gamma d\gamma ={10}^4{\pi }^2{V}^4{\left(\frac{\rho }{R_c}\right)}^2{\Psi }^2\left({\chi }_1\rho \right)I_2;\\ {\displaystyle \underset{0}{\overset{1}{\int }}{a}_1\left(\gamma \right)a_2\left(\gamma \right)\gamma d\gamma }={10}^2\pi V^2\frac{\rho }{R_c}\Psi \left({\chi }_1\rho \right)\left\{I_3+\frac{\pi V^2}{2}\Theta \left({\chi }_1\rho \right)I_4\right\};\\ {\displaystyle \underset{0}{\overset{1}{\int }}{b}_1\left(\gamma \right)}{b}_2\left(\gamma \right)\gamma d\gamma ={10}^2\frac{{\pi }^2{V}^4}{2}\frac{\rho }{R_c}\Theta \left({\chi }_1\rho \right)\Psi \left({\chi }_1\rho \right)I_5;\end{array}$

 $\begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}{a}_1^2\left(\gamma \right)\gamma d\gamma }=I_6+\pi V^2\Theta \left({\chi }_1\rho \right)I_7+\frac{{\pi }^2{V}^4}{4}{\Theta }^2\left({\chi }_1\rho \right)I_8;\\ {\displaystyle \underset{0}{\overset{1}{\int }}{b}_1^2\left(\gamma \right)\gamma d\gamma }=\frac{{\pi }^2{V}^4}{4}{\Theta }^2\left({\chi }_1\rho \right)I_6\end{array}$                  (18)

и

$I_1\equiv {\displaystyle \underset{0}{\overset{1}{\int }}{N}_1^2\left({\chi }_1\rho \gamma \right)}\gamma d\gamma ;I_2\equiv {\displaystyle \underset{0}{\overset{1}{\int }}{J}_1^2\left({\chi }_1\rho \gamma \right)\gamma d\gamma };$                                                             

$I_3\equiv {\displaystyle \underset{0}{\overset{1}{\int }}{J}_0\left({\chi }_1\rho \gamma \right)N_1\left({\chi }_1\rho \gamma \right)\gamma d\gamma };I_4\equiv {\displaystyle \underset{0}{\overset{1}{\int }}{N}_0\left({\chi }_1\rho \gamma \right)N_1\left({\chi }_1\rho \gamma \right)\gamma d\gamma };$

$I_5\equiv {\displaystyle \underset{0}{\overset{1}{\int }}{J}_0\left({\chi }_1\rho \gamma \right)J_1\left({\chi }_1\rho \gamma \right)\gamma d\gamma };I_6\equiv {\displaystyle \underset{0}{\overset{1}{\int }}{J}_0^2\left({\chi }_1\rho \gamma \right)\gamma d\gamma };$                             

$I_7\equiv {\displaystyle \underset{0}{\overset{1}{\int }}{J}_0\left({\chi }_1\rho \gamma \right)N_0\left({\chi }_1\rho \gamma \right)\gamma d\gamma };I_8\equiv {\displaystyle \underset{0}{\overset{1}{\int }}{N}_0^2\left({\chi }_1\rho \gamma \right)\gamma d\gamma }.$                (19)

Используем известные формулы из теории цилиндрических функций⁵:

$\begin{array}{l}\int Z_p^2\left(ax\right)xdx=\frac{x^2}{2}\left\{Z_p^2\left(ax\right)-Z_{p-1}\left(ax\right)Z_{p+1}\left(ax\right)\right\},Z_{-p}\left(x\right)=-{\left(-1\right)}^p{Z}_p\left(x\right),\\ \left\{J_1\left(x\right),N_1\left(x\right)\right\}=-\left\{{J^{\text{'}}}_0\left(x\right),{N^{\text{'}}}_0\left(x\right)\right\},Z_2\left(x\right)=Z_0\left(x\right)-2{Z^{\text{'}}}_1\left(x\right),\\ {\left\{N_0\left(x\right)\approx \frac{2}{\pi }{J}_0\left(x\right)\left[\ln \frac{x}{2}+C\right],{N^{\text{'}}}_0\left(x\right)\approx \frac{2}{\pi }{J^{\text{'}}}_0\left(x\right)\left[\ln \frac{x}{2}+C\right]\right\}}_{x\in \left(\mathrm{0,1}\right)},\\ C=\mathrm{0,5772156649015325...}\to C^{\text{'}}=C+\ln \frac{1}{2}\approx -\mathrm{0,116.}\end{array}$ (20)

Здесь $Z_p\left(x\right)$ – любая цилиндрическая функция порядка p от аргумента x; С – постоянная Эйлера, $f^{\prime }\left(x\right)=df\left(x\right)/dx$; p – целое число.

Запишем также легко вычисляемые интегралы (рассматриваемые как интегралы от параметра δ; Ф(х) – интеграл вероятностей ошибок):

 $\begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}\exp \left(-a{\gamma }^2\right)\ln \left(\delta \gamma \right)d\gamma }=\frac{1}{2}\sqrt{\frac{\pi }{a}}\Phi \left(\sqrt{a}\right)\ln \delta ,\\ {\displaystyle \underset{0}{\overset{1}{\int }}\exp \left(-a{\gamma }^2\right){\left[\ln \left(\delta \gamma \right)\right]}^{2}d\gamma }=\frac{1}{2}\sqrt{\frac{\pi }{a}}\Phi \left(\sqrt{a}\right){\left(\ln \delta \right)}^2,\\ {\displaystyle \underset{0}{\overset{1}{\int }}\exp \left(-a{\gamma }^2\right)\gamma \ln \left(\delta \gamma \right)}d\gamma =\frac{\left[1-\exp \left(-a\right)\right]}{2a}\ln \delta ,\\ \Phi \left(x\right)\equiv \frac{2}{\sqrt{\pi }}{\displaystyle \underset{0}{\overset{x}{\int }}\exp \left(-t^2\right)dt}.\end{array}$ (21)

Как известно, в одномодовом режиме работы волновода со ступенчатым профилем вместо функции Бесселя $J_0\left({\chi }_{1}r\right)$ можно применять функцию Гаусса (r₀ – радиус модового пятна) [34].

$\begin{array}{l}{J}_0\left({\chi }_1\rho \gamma \right)\to \exp \left(-\frac{\alpha {\gamma }^2}{2}\right)\to {J^{\text{'}}}_0\left({\chi }_1\rho \gamma \right)=\frac{1}{\left({\chi }_1\rho \right)}\frac{d}{d\gamma }\left\{\exp \left(-\frac{\alpha {\gamma }^2}{2}\right)\right\},\\ {\left[J_0^2\left({\chi }_1\rho \gamma \right)\right]}^{\text{'}}=\frac{1}{\left({\chi }_1\rho \right)}\frac{d}{d\gamma }\left\{\exp \left(-\alpha {\gamma }^2\right)\right\},\\ \alpha \equiv \frac{{\rho }^2}{r_0^2}=\mathrm{0,16}{V}^2,V\in \left(0;\mathrm{2,4}\right).\end{array}$         (22)

Распространяя формулу (22) на случай рассматриваемого градиентного профиля и комбинируя формулы (20–22), для интегралов (19) и для функций $\Theta \left({\chi }_1\rho \right)$ и $\Psi \left({\chi }_1\rho \right)$ из (14) и (16) получим:

$\begin{array}{l}{I}_1=\frac{2}{{\pi }^2}{\left\{\ln \left({\chi }_1\rho \right)-\mathrm{0,116}\right\}}^2\left\{\frac{\alpha \left(2-\alpha \right)}{{\left({\chi }_1\rho \right)}^2}-1\right\}\exp \left(-\alpha \right),\\ I_2=\frac{1}{2}\left\{\frac{\alpha \left(2-\alpha \right)}{{\left({\chi }_1\rho \right)}^2}-1\right\}\exp \left(-\alpha \right),\\ I_3=\frac{1}{2\pi \left({\chi }_1\rho \right)}\left\{\left[\ln \left({\chi }_1\rho \right)-\mathrm{0,116}\right]\left[\sqrt{\frac{\pi }{\alpha }}\Phi \left(\sqrt{\alpha }\right)-2\exp \left(-\alpha \right)\right]+\sqrt{\frac{\pi }{\alpha }}\Phi \left(\sqrt{\alpha }\right)\right\},\end{array}$

$\begin{array}{l}{I}_4=\frac{1}{{\pi }^2\left({\chi }_1\rho \right)}{\left\{\ln \left({\chi }_1\rho \right)-\mathrm{0,116}\right\}}^2\left\{\sqrt{\frac{\pi }{\alpha }}\Phi \left(\sqrt{\alpha }\right)-2\exp \left(-\alpha \right)\right\},\\ I_5=\left\{\sqrt{\frac{\pi }{\alpha }}\Phi \left(\sqrt{\alpha }\right)-2\exp \left(-\alpha \right)\right\},\\ I_6=\frac{\left\{1-\exp \left(-\alpha \right)\right\}}{2\alpha },\\ I_7=\frac{1}{\pi \alpha }\left\{1-\exp \left(-\alpha \right)\right\}\left\{\ln \left({\chi }_1\rho \right)-\mathrm{0,116}\right\},\end{array}$

$\begin{array}{l}{I}_8=\frac{2}{{\pi }^2}{\left\{\ln \left({\chi }_1\rho \right)-\mathrm{0,116}\right\}}^2\left\{1+\frac{{\alpha }^2}{{\left({\chi }_1\rho \right)}^2}\right\}\exp \left(-\alpha \right),\\ \Psi \left({\chi }_1\rho \right)=\frac{\left\{1-\left(1+\alpha \right)\exp \left(-\alpha \right)\right\}}{\alpha \left({\chi }_1\rho \right)},\\ \Theta \left({\chi }_1\rho \right)\to \Theta \left(\alpha \right)={\displaystyle \underset{0}{\overset{1}{\int }}\exp \left(-\alpha {\gamma }^2\right)\gamma h\left(\gamma \right)d\gamma }.\end{array}$

Так как использовали формулы (22) для упрощения вычислений в рассматриваемом одномодовом режиме, то считаем, что при двух описаниях поток энергии через поперечное сечение одинаков:

${\displaystyle \underset{0}{\overset{1}{\int }}{J}_0^2\left({\chi }_1\rho \gamma \right)\gamma d\gamma }\equiv {\displaystyle \underset{0}{\overset{1}{\int }}\exp \left(-\alpha {\gamma }^2\right)\gamma d\gamma }=\frac{1}{2\alpha }\left\{1-\exp \left(-\alpha \right)\right\}$ .

С другой стороны, для левой части этого соотношения, согласно (15) и (18):

$\begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}{J}_0^2\left({\chi }_1\rho \gamma \right)\gamma d\gamma }=\frac{1}{2}{\left\{J_0^2\left({\chi }_1\rho \gamma \right)+\frac{1}{{\left({\chi }_1\rho \right)}^2}{\left[\frac{d}{d\gamma }{J}_0\left({\chi }_1\rho \gamma \right)\right]}^2\right\}}_{\gamma =1}=\\ =\left\{J_0\left(\chi \rho \to \exp \left(-\alpha /2\right)\right)\right\}=\frac{1}{2}\left\{1+\frac{{\alpha }^2}{{\left({\chi }_1\rho \right)}^2}\right\}\exp \left(-\alpha \right).\end{array}$

Сравнивая правые части, находим (подробней в работе [15]):

$\left({\chi }_1\rho \right)=\left({\chi }_1\rho \right)\left(V\right)={\left\{\frac{{\alpha }^3}{\exp \alpha -1-\alpha }\right\}}^{1/2}.$

Используя формулы (14), (17‒18), для (13) получаем $W_{str-curv}=W_{str}-W_{curv}$:

$\begin{array}{l}q\left(\alpha ,\beta \right)\equiv \frac{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|A_{curv}\left(\gamma \right)\right|}^2\gamma d\gamma }}{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|A_{str}\left(\gamma \right)\right|}^2\gamma d\gamma }}=1-\frac{W_{str-curv}}{W_{str}},\\ W_{str}\equiv \frac{\left[1-\exp \left(-\alpha \right)\right]}{2\alpha }\left[1+2V^2\Theta \left(\alpha \right)w_3+\frac{{\pi }^2{V}^4}{4}{\Theta }^2\left(\alpha \right)\right]+\frac{V^4}{2}{\Theta }^2\left(\alpha \right)\exp \left(-\alpha \right)w_3^2{w}_5,\end{array}$

$\begin{array}{l}{W}_{str-curv}\equiv {10}^2{V}^2\beta w_1\left\{{\pi }^2{V}^2{w}_4\Theta \left(\alpha \right)-{\left[\frac{\exp \left(\alpha \right)-1-\alpha }{{\alpha }^3}\right]}^{1/2}{w}_3\times \right.\\ \left.\times \left[w_3{w}_4\left(1+w_3{V}^2\Theta \left(\alpha \right)\right)+\sqrt{\frac{\pi }{\alpha }}\Phi \left(\sqrt{\alpha }\right)\right]-{10}^2{V}^2\beta w_1{w}_2\exp \left(-\alpha \right)\left(2w_3^2-\frac{{\pi }^2}{2}\right)\right\}\end{array}$ , (23)

где

$\begin{array}{l}{w}_1\left(\alpha \right)\equiv {\left[\frac{\exp \left(\alpha \right)-1-\alpha }{\alpha }\right]}^{1/2}\frac{\left[1-\left(1+\alpha \right)\exp \left(-\alpha \right)\right]}{{\alpha }^2},\\ w_2\left(\alpha \right)\equiv \frac{\left(2-\alpha \right)\left[\exp \left(\alpha \right)-1-\alpha \right]}{{\alpha }^2}-1,\\ w_3\left(\alpha \right)\equiv \frac{1}{2}\ln \left[\frac{{\alpha }^3}{\exp \left(\alpha \right)-1-\alpha }\right]-\mathrm{0,116},\\ w_4\left(\alpha \right)\equiv \sqrt{\frac{\pi }{\alpha }}\Phi \left(\sqrt{\alpha }\right)-2\exp \left(-\alpha \right),\end{array}$

  $\begin{array}{l}{w}_5\left(\alpha \right)\equiv 1+\frac{\left[\exp \left(\alpha \right)-1-\alpha \right]}{\alpha },\\ \Theta \left(\alpha \right)=\underset{0}{\overset{1}{\int }}\exp \left(-\alpha {\gamma }^2\right)\gamma h\left(\gamma \right)d\gamma ,\\ \Phi \left(x\right)\equiv \frac{2}{\sqrt{\pi }}\underset{0}{\overset{x}{\int }}\exp \left(-t^2\right)dt,\end{array}$                                                             

 $\alpha =\mathrm{0,16}{V}^2,\beta \equiv \rho /R_c<<1,V\in \left(0;\mathrm{2,4}\right).$                                                               (24)

Таким образом, полученные формулы (23‒24) описывают изменение энергии в волокне при малых изгибах для произвольного градиентного профиля в первом приближении.

Чтобы представить результат наглядно, необходимо знание конкретного профиля, описываемого функцией h(γ), входящей в величину Θ(α). Поскольку квадратичный профиль наиболее приближен к реально используемым градиентным профилям, то в качестве примера численные расчеты произведем именно для такого профиля, соответствующего функции h(γ)=γ² (формулы (3), (10)). В этом случае для Θ(α) из (20) получаем:

 $\Theta \left(\alpha \right)\Rightarrow \left(h\left(\gamma \right)={\gamma }^2\right)\Rightarrow {\displaystyle \underset{0}{\overset{1}{\int }}\exp \left(-\alpha {\gamma }^2\right){\gamma }^{3}d\gamma }=\frac{\left\{1-\left(1+\alpha \right)\exp \left(-\alpha \right)\right\}}{2\alpha }.$        (25)

Остался вопрос с выбором значений параметра $\beta =\rho /R_c$. Исходим из того, что для оптоволоконного кабеля, согласно техническому руководству, существует общепринятое соотношение $R_{c\left(\min \right)}\approx 20\times D_{cable}$ между диаметром кабеля D_cable и минимальным радиусом кривизны Rc_(min). С другой стороны, для одномодовых волокон, также согласно техническому руководству, существует соотношение $d/D_{cable}\approx \left(8÷10\right)/125$ между D_cable и диаметром волокна d = 2p. Из этих соотношений находим:

$R_c>R_{c\left(\min \right)}\Rightarrow \beta =\frac{\rho }{R_c}<\frac{\rho }{R_{c\left(\min \right)}}\approx \frac{\left(8÷10\right)}{5000}=\left(\mathrm{1,16}÷2\right)\cdot {10}^{-3}.$             (26)

На этом основании выберем для β значения:

$\beta \in \left(0;\mathrm{0,4};\mathrm{0,8};\mathrm{1,2};\mathrm{1,6};2\right)\cdot {10}^{-3}$.                               (27)

С использованием формул (23–27) проведены вычисления. Они приводят к зависимости относительной энергии q от параметра β = ρ/Rc для различных значений волноводного параметра V при высоте профиля Δ ≈ 0,005 (рис. 2).

Рис. 2. Зависимость отношения q от параметра β для различных значений волноводного параметра V: (кривая 1 – V₁ = 0,5; кривая 2 – V₂ = 0,9; кривая 3 – V₃ = 1,3; кривая 4 – V₄ = 1,7)

Fig. 2.  Dependence of the ratio q on the parameter β for different values of the waveguide parameter V: (curve 1 – V₁ = 0.5; curve 2 – V₂ = 0.9; curve 3 – V₃ = 1.3; curve 4 – V₄ = 1.7)

Источник: составлено автором.

Source: the diagram was drawn up by the authors of the article.

На рисунке 2 показана зависимость отношения q от параметра β для различных значений волноводного параметра V: (кривая 1 – V₁ = 0,5; кривая 2 – V₂  = 0,9; кривая 3 – V₃ = 1,3; кривая 4 – V₄ = 1,7).

Обсуждение и заключение

В первом приближении для квадратичного профиля построены зависимости относительной энергии q от параметра β при различных значениях волноводного параметра V. Энергия q убывает с увеличением β при этом тем быстрее, чем больше V. Предложенный метод исследования влияния микроизгибов на передаваемую энергию – замена изогнутого участка на эквивалентный прямолинейный – позволяет в конечном итоге анализировать энергетические потери в зависимости от радиуса изгиба не только для рассмотренного квадратичного, но и для любого градиентного профиля в первом приближении методом функции Грина, что может быть использовано как при конструировании волноводов с заранее заданными свойствами, так и в различных технических приложениях (волоконно-оптические датчики в технике и медицине, проблема безопасности передачи данных и т. д.).

¹         Снайдер А., Лав Дж. Теория оптических волноводов / пер. с англ. под ред. Е. М. Дианова, В. В. Шевченко. М. : Радио и связь, 1987. 656 с.

²         Унгер Х. Г. Планарные и волоконные оптические волноводы / пер. с англ. под ред. В. В. Шевченко. М.: Мир, 1980. 656 с.

³        Okamoto K. Fundamentals of optical waveguides. Elsevier Inc, 2006. 561 p. https://doi.org/10.1016/B978-0-12-525096-2.X5000-4

⁴         Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. СПб. : БХВ-Петербург, 2011. 1232 с.

⁵       Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений.

Sobre autores

Vyacheslav Gladkikh

Far Eastern Branch of the Russian Academy of Sciences

Email: gladkih@as.khb.ru
ORCID ID: 0000-0002-3922-9609
Researcher ID: GLU-2712-2022

Cand.Sc. (Phys.-Math.), Senior Researcher, Computing Center

65 Kim Yu Chen St., Khabarovsk 680000, Russian Federation

Victor Vlasenko

Far Eastern Branch of the Russian Academy of Sciences

Autor responsável pela correspondência
Email: vlasenko@as.khb.ru
ORCID ID: 0000-0001-7782-4532
Researcher ID: E-2432-2019

Cand.Sc. (Phys.-Math.), Scientific Secretary, Computing Center

5 Kim Yu Chen St., Khabarovsk 680000, Russian Federation

Bibliografia

Arquivos suplementares